.png)
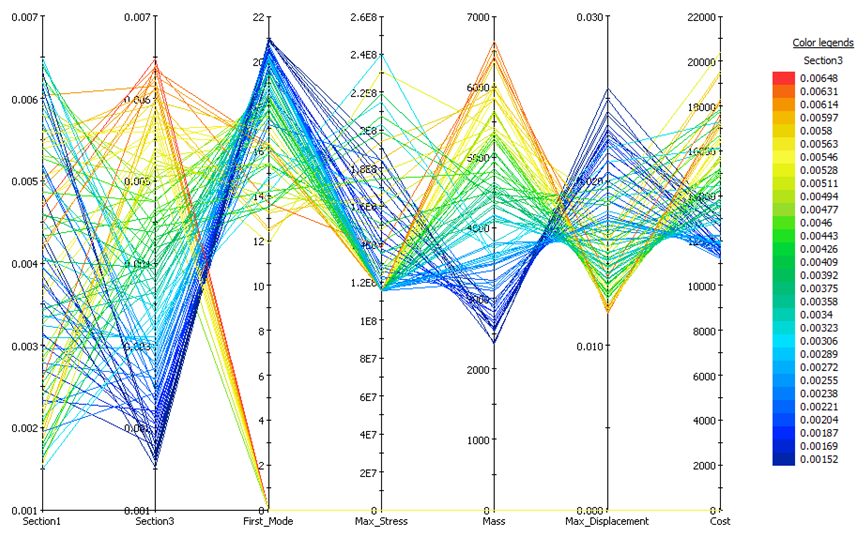
數學最佳化

.jpg)
 電話
電話
 原廠資訊
原廠資訊
研究是提供給高山探險者、科學家,數學家,以及在我們的日常生活中每一個人。強大的計算能力提供了極大的理由發展數學最佳化的方法,來解決人類很難解決的問題。通過安排一個智能評估,這些可靠的方法能夠有效地追踪函數的極限。今天,多學科最佳化方法在具挑戰性的工程和規劃項目決策過程中,提供關鍵信息。
最佳化的目標是找到該決定模型,得出了眾多全面和局部最優的最佳解決方案。多目標最佳化是一個活躍的研究領域,聚焦在眾多工程、科學和經濟學應用上。
不再有試錯
傳統上,設計工程師從一組輸入的變量開始。當花費時間手動改進設計,他們試圖判斷部分衝突的屬性,如重量、成本和產品性能特性的影響。

使用 Optimus 數值最佳化軟體,Noesis 方案顛覆了整個過程。首先,用戶設定所需的產出目標。然後 Optimus 在後台工作,採用先進的迭代和最佳化方法,以確定符合您的設計標準輸入值。在軟件中包含的算法,確保找到最佳的產品屬性。
基於模擬的數值最佳化
在科學與工程中,模擬是一個強大的工具,可以預測物理系統的行為。此外,算法和計算模擬硬體的進展有了進一步的改善。當今的模擬工具已更加實際地在處理複雜的設計問題,為確定大系統參數,最大限度地提高特定目標。
這種設計上的問題事實上就是最佳化問題。取而代之的最佳化數學表達式,最佳化對待模擬模型如黑箱最佳化。基於模擬最佳化過程編入到 Optimus 中,一個數值最佳化的軟體解決方案,調整模擬模型的輸入變量,來確定達到最好水平的結果。
通常,基於模擬的最佳化設置因為自身的大尺寸,可能會產生不精確的導數,以及會耗費大量的時間。這些都對其構成了嚴峻的挑戰。許多相互矛盾的目標必須同時最佳化,這使得它更有挑戰性。
.bmp)
Optimus 結合了標準圖形化界面,可以實現對單個或多個目標的最佳化,以及任何自定義算法方案。這個自定義功能, 允許您在個案的基礎上研究算法,選擇最合適你的方案算法。
.bmp)
.bmp)
數值最佳化的分類
基於對目標函數的個數,Optimus 數值最佳化方法可劃分為子區:
基於對目標函數的個數,Optimus 數值最佳化方法可劃分為子區:
並可以根據搜索方法,Optimus 將其最佳化方法歸類為:
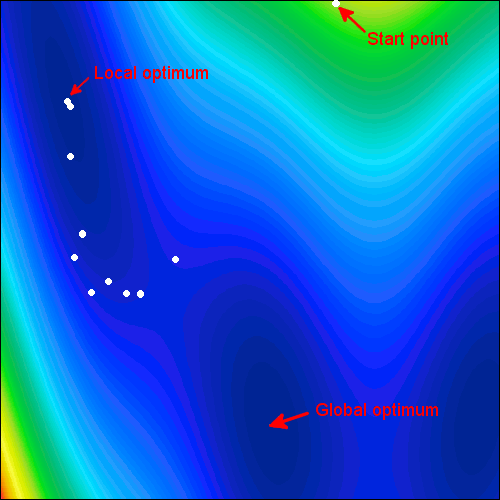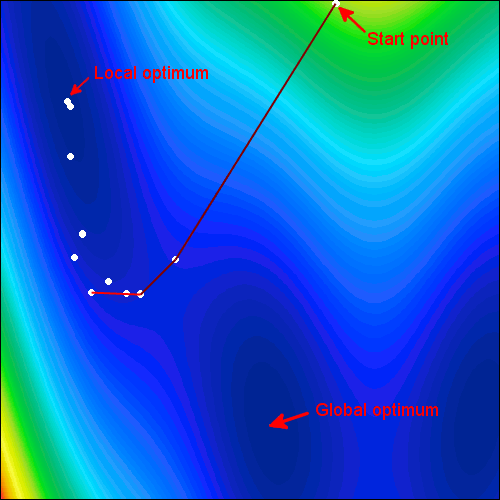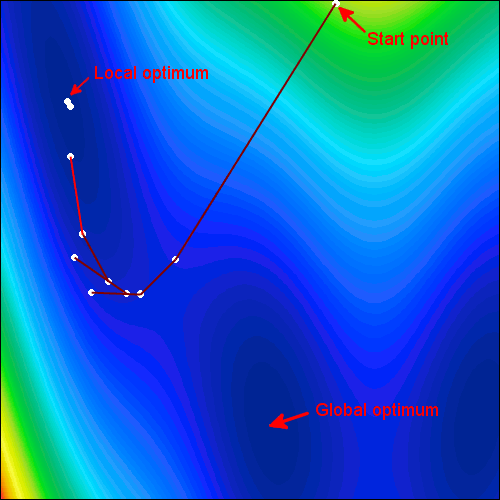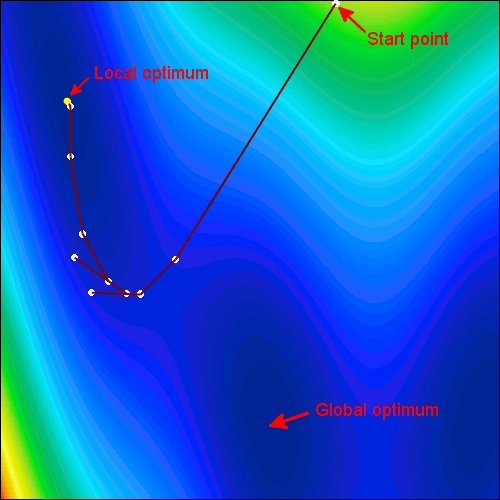
- 局部最佳化方法:局部最佳化方法搜索,基於一個最佳的本地信息,比如梯度和幾何信息的最佳化問題。局部最佳可以使用這些算法被發現。
- 全局最佳化方法:全局最佳化搜索基於,關於全局信息的最佳化問題。這些通常是基於概率的搜索方法。這些方法有很好的可能性找到全局最佳,但是不能保證。
- 混合最佳化方法混合最佳化方法以一種無縫隙的方式連接本地和全球。這些通常依賴於響應面近似,以最小的努力找到全局最佳。
Optimus 結合了標準圖形化界面,可以實現對單個或多個目標的最佳化,以及任何自定義算法方案。這個自定義功能, 允許您在個案的基礎上研究算法,選擇最合適你的方案算法。
.bmp)
該插件的功能是基於一個簡單文件為基礎的系統,為您提供了巨大的方便,不論您使用什麼樣的程式語言,很容易地把自己的最佳化算法融入 Optimus 多學科最佳化軟體。 結果被存儲在標準 Optimus 數據庫。以及完全支持其後所有 Optimus 的後處理功能。
該 eArtius - Optimus 插件提供了四種創新的多目標最佳化算法。eArtius 算法利用梯度估計(DDRSM),以及多目標最佳化技術,如帕累托邊界、混合型遺傳算法、梯度技術導向的最佳化。這些技術之間的協同作用使得在由其它方法所需時間的僅一小部分時間內,就能解決高度尺寸多目標的問題。
-
多梯度瀏覽器(MGE)算法使用常規方法的最佳化實踐。它從一個初始點迭代訪問帕累托邊界,直到帕累托最佳點被發現。然後它會佔據一個初始點,再次迭代訪問,等等
-
多梯度探路者(MGP)算法使用帕累托邊界作為多目標最佳化的搜索空間,並以這種方式在帕累托邊界引導最佳化。帕累托邊界導向手段最佳化表示,搜索算法的步驟沿著帕累托邊界,從給定的初始帕累托最佳點朝向期望的帕累托最佳點
-
混合型多梯度瀏覽器(HMGE)結合了GA架構按照一種獨特的eArtius方法來估算梯度。以這種方式,HMGE綜合了優點並避免兩個主要最佳化方法的弱點:梯度為基礎的技術和遺傳算法(GAs)
-
混合型多梯度探路者(HMGP)算法是一種新的多目標最佳化算法,它結合了 MGP(多梯度探路者)算法與遺傳算法(GA)的元素。
-
所有eArtius最佳化算法,使用在 eArtius 新開發的梯度估計方法:動態維度響應面法(DDRSM)。DDRSM對低維和高維任務同樣有效。不管任務維度,它僅需要5-7模型評估來估算梯度。
業務聯絡 (03) 6118-668 轉 220 姜小姐
思渤科技提供完整的產品諮詢、技術支援、產品訓練及售後服務,歡迎立即電洽思渤科技 03-6118-668 或來信。